电路量子电动力学 circuit QED | 约瑟夫森结和超导比特

前言

在上一篇文章中我先容了QED中的标准量子化操纵（文章链接鄙人方）。有了这一铺垫，我们便可以真正从量子电动力学角度动身研讨电路的量子化行为。

假如读者对超导量子计较的架构有大致的领会就会晓得，全部框架的焦点就是超导比特中的约瑟夫森结。那末为什么约瑟夫森结这么重要？不利用约瑟夫森结难道就不能做超导量子计较？答案简直是不可，这是由于约瑟夫森结是一个无损的非线性电路元件，简单来说可以将其视为一种非线性电感。这里我需要别离夸大”无损“和”非线性“两个概念的意义：

首先，非线性原件在现代电路设想中并很多见，可是由于量子态的懦弱性，我们需要极力避免各类能够的消耗，这也是为什么我们要利用超导电路的缘由之一。

其次，即使非线性电路元件有很多，可是想要在单光子级别就能明显观察到的非线性照旧很是少。约瑟夫森结的道理是超导体中库伯对隧穿电介质发生等效势能，可以发生单光子级此外非线性。

上面两点说的是约瑟夫森结在无损非线性元件中的上风，但我们还需要斟酌一个题目：为什么我们需要非线性？我感觉假如要回答这个题目，可以从非线性光学中获得比力intuitive的了解：给你一个线性的光学系统和几个典范光源，你不管若何也没法发生跳脱出典范电动力学理论可以描写的范围；而假如给你一个具有非线性的光学系统，即使照旧只要典范光源，在一些特别的情况下便可以发生量孜扌为，例如二阶大概三阶非线性可以发生纠缠光子对。简单来说，对于线性系统的行为，典范理论描写足矣；而对于非线性系统，即使利用典范泵浦也可以发生需要量子理论才能描写的现象，才有实现量子计较的能够。

以上部分是写在正式定量先容约瑟夫森结之前的一些小我了解，与后续内容关系不大，接待交换斧正。

约瑟夫森结（Josephson Junction）

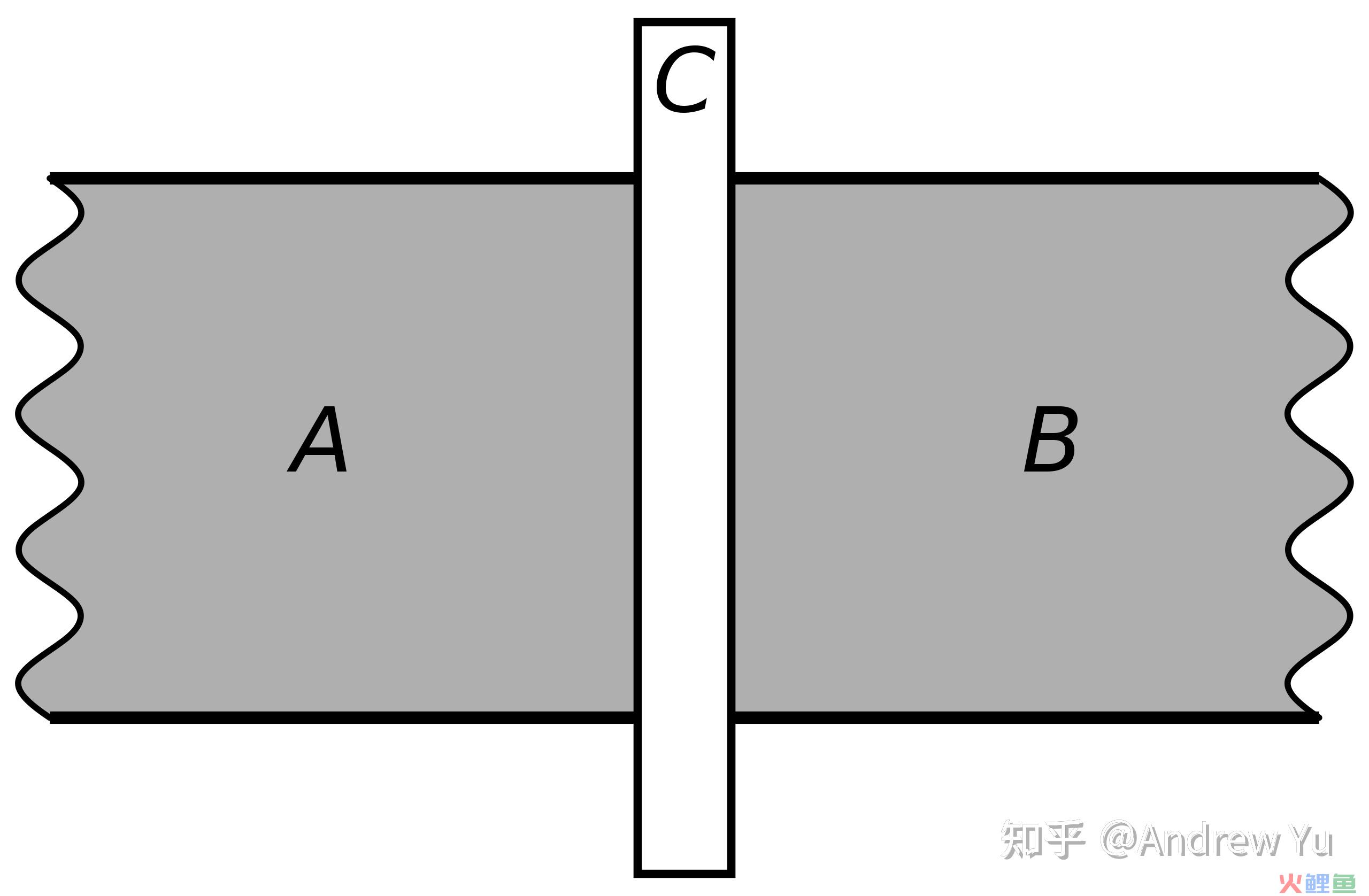
约瑟夫森结的结构以下图，A和B是超导体，C是绝缘电介质，大概说是非超导体。一般情况下，在这类结构两头加上电压是不会有电流的，由于串联是断路。但是当C充足薄时，电子（Cooper对）便可以在AB之间发生隧穿，从而由一端流到另一端，发生电流。具体推导其中的物理实在还是比力tricky的，是以在后文中我将只关注约瑟夫森结的一些结论，跳过物理细节。

流经约瑟夫森结的电流由两个参数决议：结临界电流 I_c 和结两侧超导体中电子波函数相位差 \varphi : I=I_c\sin\varphi\\ 而相位差与结两真个电压具有以下关系： \frac{d\varphi}{dt}=2\pi\frac{V}{\Phi_0},\ \Phi_0 = \frac{\hbar}{2e}\\ 其中 \Phi_0 是Cooper对对应的磁通量子，对上式积分有 \varphi(t) = 2\pi\frac{\int_{-\infty}^tV(\tau)d\tau}{\Phi_0} = 2\pi\frac{\Phi(t)}{\Phi_0}\\ \Phi(t) 就是我在上篇文章中界说的磁通（flux）固然，既然是相位，我们需要对上式取mod 2\pi .到这一步我们可以看出，约瑟夫森电流 I 和结的磁通 \Phi(t) 是有定量关系的： I (t)= I_c\sin(2\pi\frac{\Phi(t)}{\Phi_0})\\ 是以我们可以计较出约瑟夫森结的等效电感： L_J(\Phi)=\left(\frac{\partial I}{\partial \Phi}\right)^{-1}=\frac{\Phi_0}{2 \pi I_c} \frac{1}{\cos \left(2 \pi \Phi / \Phi_0\right)}\\ 可以发现这是磁通的函数（固然，也是电流的函数），而常见的电感都具有常数电感值，是以约瑟夫森结不具有常数电感，是一个非线性电感（磁通和电流不是线性相关）。根据能量守恒，我们计较出约瑟夫森结作为一个电感所存储的磁场能： E = \int_{-\infty}^tV(\tau)I(\tau)d\tau\\ 带入计较得 E=I_c \int d t\left(\frac{d \Phi}{d t}\right) \sin \left(\frac{2 \pi}{\Phi_0} \Phi\right)=-E_J \cos \left(\frac{2 \pi}{\Phi_0} \Phi\right)\\ 这里界说了约瑟夫森能 E_J = \Phi_0I_c/2\pi .

但是我们从另一个角度看约瑟夫森结，这似乎又是一个很是典型的电容结构。简直，约瑟夫森结是有电容值的，但同时这类电容又会经过隧穿电流”漏电“，所以当我们计较约瑟夫森结的总能量时常常是从电容值和漏电电流（大概电容值和结两头相位差）动手，由于电流和相位差在上述推导中都不依靠于电容。虽然如此，处置约瑟夫森结照旧是比力辣手的，是以我们一般在特定的外电路大概外电磁情况下计较全部系统的哈密顿量，而这就会触及约瑟夫森结的耦公道论。

约瑟夫森结的耦合

与电压源的耦合

我们斟酌一种常见的情况，电路以下，图中的”X“形原件就是约瑟夫森结。想要写出这一个耦合系统的哈密顿量，我们首先界说几个物理量： \Phi_A,\Phi_B,\Phi_C . 他们别离是图中标出的几个元件的磁通。在后续的推导中我们会发现这几个磁通并不是自力的，可是在推导中会起到帮助感化。

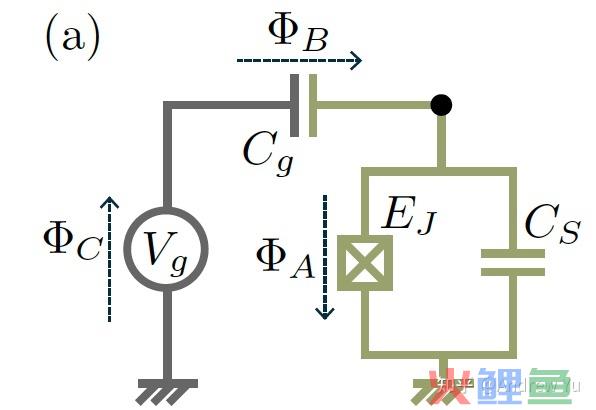
我们将约瑟夫森结视为漏电电容，电容值为 C_J ，结两头相位差为 \varphi_A 。首先，磁通C由地震身，磁通A由地结尾，磁通B链接磁通A和C，是以他们必定满足 \Phi_A+\Phi_B+\Phi_C = \int_{-\infty}^t(V_A+V_B+V_C)d\tau = 0\\所以我们可以消掉 \Phi_B .界说绿色电路的总电容 C_\Sigma = C_J+C_S ， C_J 和 C_S 别离为约瑟夫森结和与其并联的电容。以结磁通 \Phi_A,\Phi_C 为广义坐标，电场能为动能，磁场能为势能： T=\frac{C_{\Sigma}}{2} \dot{\Phi}_A^2+\frac{C_g}{2}\left(\dot{\Phi}_A+\dot{\Phi}_C\right)^2\\ V = -E_J\cos(\varphi_A)\\ 则系统的拉氏量为 \mathcal{L}_T=T-V=\frac{C_{\Sigma}}{2} \dot{\Phi}_A^2+\frac{C_g}{2}\left(\dot{\Phi}_A+\dot{\Phi}_C\right)^2+E_J \cos \varphi_A\\ 对应可以算出系统的广义动量 Q_A=\partial \mathcal{L}_T / \partial \dot{\Phi}_A=\left(C_{\Sigma}+C_g\right) \dot{\Phi}_A+C_g \dot{\Phi}_C ，哈密顿量是以为 H_T=Q_A \dot{\Phi}_A-\mathcal{L}_T\\对于图中的情况， \Phi_C 的表达式就很是简单，为 V_gt ，是以广义动量为 Q_A=\partial \mathcal{L}_T / \partial \dot{\Phi}_A=\left(C_{\Sigma}+C_g\right) \dot{\Phi}_A+C_g V_g\\对应哈密顿量为 \begin{align} H_T&=\frac{\left(Q_A-C_g V_g\right)^2}{2\left(C_{\Sigma}+C_g\right)}-E_J \cos \varphi_A\\ &\approx\frac{\left(Q_A-C_g V_g\right)^2}{2C_{\Sigma}}-E_J \cos \varphi_A\\ \end{align}\\上式中的约即是对应 C_g\ll C_\Sigma ，这一近似在大部分情况下建立，由于我们凡是希望用于耦合的电容只管小，不要对原本的自力系统发生过大的影响。

与LC电路耦合

另一种常见的耦合系统是一个约瑟夫森结与电容 C_S 并联，然后经过 C_g 与另一个LC电路耦合，电路见下图（部分电路元件没有标出，我也不晓得review里面为什么不标）

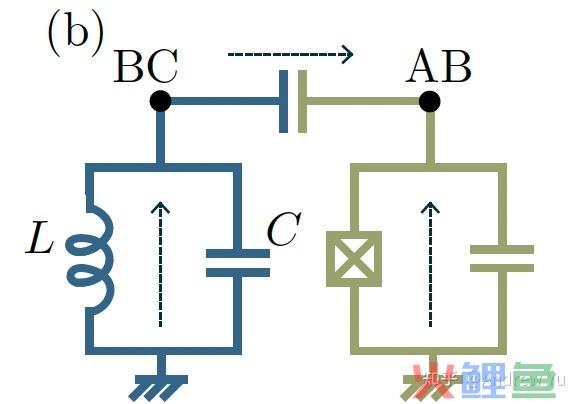
界说磁通 \Phi_A 为右侧绿色电路的磁通， \Phi_C 为左侧蓝色电路磁通，偏向均以图中箭头标出，则我们很轻易算出耦合电容上的磁通 \Phi_B=\Phi_A-\Phi_C . 图中节点BC处电流守恒，而且略加观察会发现我们可以用 \Phi_A 和 \Phi_C 暗示出LC电路和耦合电容的电流，加入持续条件获得以下约束： C \ddot{\Phi}_C+\frac{\Phi_C}{L}=C_g\left(\ddot{\Phi}_A-\ddot{\Phi}_C\right)\\左侧为LC电路输出电流，右侧为耦合电容向右的电流。这样我们就获得了约瑟夫森结与LC电路耦合的约束条件了。我们回首上一小节中推导出的耦合约瑟夫森结的拉氏量，其形式为 \mathcal{L}_T=T-V=\frac{C_{\Sigma}}{2} \dot{\Phi}_A^2+\frac{C_g}{2}\left(\dot{\Phi}_A+\dot{\Phi}_C\right)^2+E_J \cos \varphi_A\\再加上LC电路的拉氏量 \mathcal{L}_{L C}=\frac{C}{2} \dot{\Phi}_C^2-\frac{1}{2 L} \Phi_C 就获得了系统总拉氏量 \mathcal{L}=\mathcal{L}_T+\mathcal{L}_{LC}\\这一拉氏量由广义坐标 \Phi_A,\Phi_C 和广义速度 \dot{\Phi}_A,\dot{\Phi}_C 暗示，具体展开的形式为 \mathcal{L}=\frac{C_\Sigma+C_g}{2}\dot{\Phi}_A^2+\frac{C+C_g}{2}\dot{\Phi}_C^2+C_g\dot{\Phi}_A\dot{\Phi}_C+E_J \cos \varphi_A-\frac{1}{2L}\Phi_C\\从中算出广义动量 Q_A = \frac{\partial\mathcal{L}}{\partial \dot{\Phi_A}} = (C_\Sigma+C_g)\dot{\Phi_A}+C_g\dot{\Phi}_C\\ Q_C = \frac{\partial\mathcal{L}}{\partial \dot{\Phi_C}} =(C+C_g)\dot{\Phi_A}+C_g\dot{\Phi}_A\\而且可以获得系统哈密顿量： H=\frac{\left(C+C_g\right)}{2 \bar{C}^2} Q_A^2+\frac{C_g}{\bar{C}^2} Q_A Q_C-E_J \cos \varphi_A +\frac{\left(C_{\Sigma}+C_g\right)}{2 \bar{C}^2} Q_C^2+\frac{\Phi_C}{2 L} \\

其中 \bar{C}^2=C_g C_{\Sigma}+C_g C+C_{\Sigma} C 。这里我们可以稍微观察一下今朝获得的成果。首先，两个广义动量并不是仅仅别离代表LC电路和约瑟夫森结电路，而是由两者组合而成。这实在并不意外，由于两者存在耦合。其次，虽然我们用A和C的广义坐标和动量暗示了系统哈密顿量，可是我们仍要清楚在推导进程中我们获得了LC电路和约瑟夫森结电路的磁通约束关系，是以两者的动力学进程是相互影响的。

假如继续取近似 C_g\ll C_\Sigma,C ，则可以简化上述表达式为 H \simeq \frac{\left(Q_A+\frac{C_g}{C} Q_C\right)^2}{2 C_{\Sigma}}-E_J \cos \varphi_A+H_{L C}\\ H_{LC} = \frac{Q_C^2}{2C}+\frac{\Phi_C^2}{2L}\\关于这一哈密顿量还有另一种常见的形式：界说 \hat{n}=\hat{Q}_A / 2 e, \hat{n}_r=\left(C_g / C\right) \hat{Q}_C / 2 e ，从物理意义上讲两者可以了解为约瑟夫森结的隧穿Cooper对数目和由耦合致使的隧穿Cooper对数目。固然这只是很是唯象的了解，由于系统是耦合的，不能简单拆成两个系吐溷丁感化之和。在这类界说下，哈密顿量改写为 \hat{H}=4 E_C\left(\hat{n}+\hat{n}_r\right)^2-E_J \cos \hat{\varphi}+H_{LC}\\其中 E_C = e^2/2C_\Sigma .至此，我们获得了在文献中最多见的耦合约瑟夫森结哈密顿量。

超导量子比特（superconducting qubit）

下图即为超导量子比特（后文简称超导比特）的电路图，实在就是一个约瑟夫森结和一个电容并联而成。

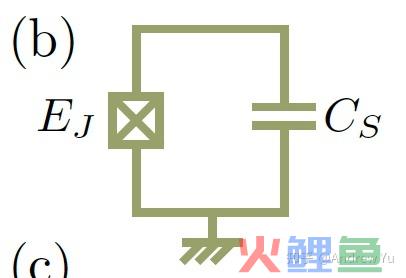
按照上一节的推导，我们可以写出其哈密顿量 \begin{aligned} \hat{H}_{\mathrm{T}} &=\frac{\left(\hat{Q}-Q_g\right)^2}{2 C_{\Sigma}}-E_J \cos \left(\frac{2 \pi}{\Phi_0} \hat{\Phi}\right) \\ &=4 E_C\left(\hat{n}-n_g\right)^2-E_J \cos \hat{\varphi} \end{aligned}\\其中 n_g 代表与超导比特与外界的电容耦合致使的额外电荷。这一电荷是不成避免的，由于不存在完全封锁的量子系统（假如真有的话我们也没法利用这一量子比特，由于完全没法对其施加任何影响）。在这一哈密顿量中，隧穿cooper对数目 \hat{n} 和约瑟夫森结相位 \hat{\varphi} 是一对共轭的变量（最多相差一个常系数）

按照制造出来的qubit的 E_J/E_C 的数值，我们可以将超导比特分为几类，其中比力常见的有Charge qubit，其 E_J/E_C\approx1\sim10 ，还有Transmon，其 E_J/E_C\approx50\sim80 。为什么要依照这类比值分类呢？主如果为了避免耦合致使的电荷涨落发生退相关。超导比特和外界电磁场发生的形式会在哈密顿量中增加一个 n_g项，而当外界有电荷涨落时，对应的超导比特中的耦合电荷也会发生涨落，从而致使其能级发生移动。由于涨落是随机的，在这一进程中系统的相位也会随机波动，终极致使退相关。从哈密顿量中可以看出这一电荷涨落影响的是电容能量部分，是以假如我们将电容增大，从而减小 E_C ，虽然这样 \hat{n} 的涨落会增大，可是 n_g 与超导比特的电容无关，只与外电路和耦合电容有关，是以 n_g 涨落带来的总能量改变就会获得抑制，从而削弱退相关。下图展现了分歧比值下系统能级对耦合电荷涨落的响应，可以发现Transmon（最右侧）几近不受影响，对应的就不轻易退相关。固然，这也是有价格的，而价格就是会致使超导比特作为一个非简谐振子的非简谐性anharmonicity（简单来说就是能级之间能量差的不均一性）削弱，不外这一下降在可接管范围内。这也就是为什么现在做量子计较的几近都是用Transmon。

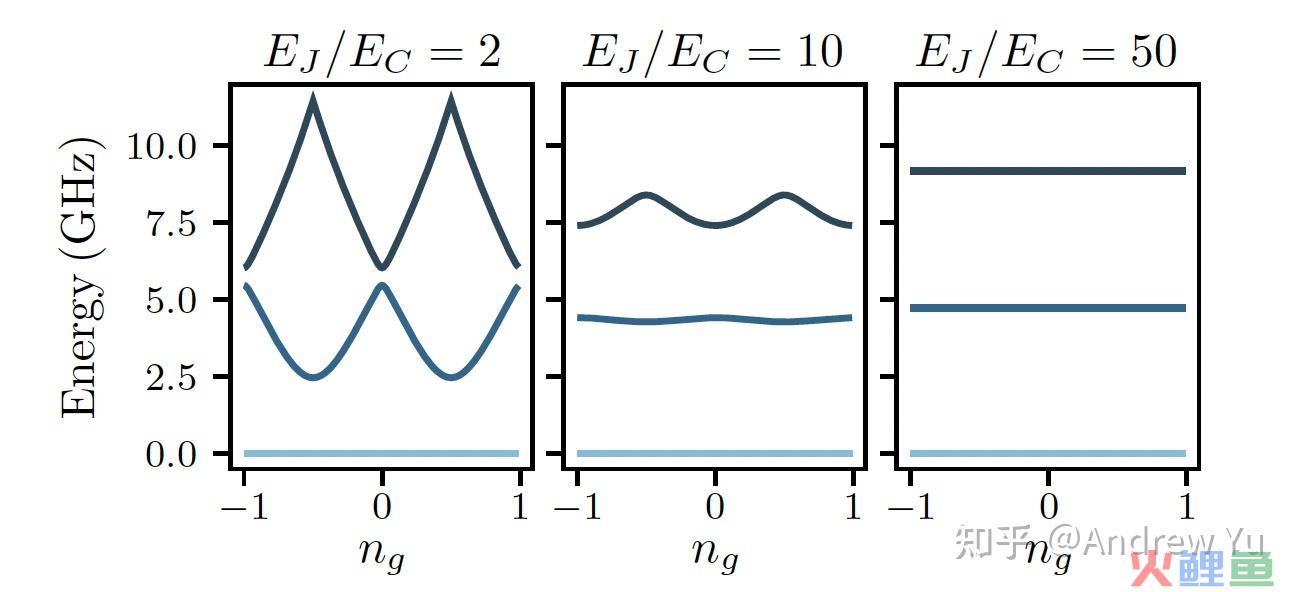
由于Transmon的这类上风，在后文中我们都假定在是在Transmon范围内会商量子比特。 E_J\gg E_c 致使的成果就是 \sigma(n)\gg\sigma(\varphi) ，即电荷的零点涨落远大于相位的零点涨落。这里的零点涨落与之条件到的电容耦合致使的涨落有一些区分，前者是超导比特本身由不肯定性致使的涨落，后者是外电路中电荷的零点涨落对超导比特施加的影响（一种间接的涨落）。由于相位的零点涨落很是小，我们可以对相位做小量展开： \hat{H}_{\mathrm{q}}=4 E_C \hat{n}^2+\frac{1}{2} E_J \hat{\varphi}^2-E_J\left(\cos \hat{\varphi}+\frac{1}{2} \hat{\varphi}^2\right)\\这里我为了简介疏忽了超导比特的电容耦合发生的电荷，即 n_g ，可是对于一般的系统还是要加上的，否则就没法对超导比特停止量子操纵和丈量。由于 \sigma(\varphi)\ll2\pi ,我们有 \hat{H}_{\mathrm{q}}=4 E_C \hat{n}^2+\frac{1}{2} E_J \hat{\varphi}^2-\frac{1}{4 !} E_J \hat{\varphi}^4\\前两项就是一般的线性谐振电路哈密顿量，第三项代表超导比特作为一个非简谐振子的非简谐项。对前两项引入升降算符 \begin{aligned} \hat{\varphi} &=\left(\frac{2 E_C}{E_J}\right)^{1 / 4}\left(\hat{b}^{\dagger}+\hat{b}\right)\\ \hat{n} &=\frac{i}{2}\left(\frac{E_J}{2 E_C}\right)^{1 / 4}\left(\hat{b}^{\dagger}-\hat{b}\right) \end{aligned}\\ 然后我们便可以将哈密顿量写为更简洁的形式 \begin{aligned} \hat{H}_{\mathrm{q}} &=\sqrt{8 E_C E_J} \hat{b}^{\dagger} \hat{b}-\frac{E_C}{12}\left(\hat{b}^{\dagger}+\hat{b}\right)^4 \\ & \approx \hbar \omega_q \hat{b}^{\dagger} \hat{b}-\frac{E_C}{2} \hat{b}^{\dagger} \hat{b}^{\dagger} \hat{b} \hat{b} \end{aligned}\\其中的约等号是在扭转波近似（rotating wave approximation，RWA）下建立，即疏忽哈密顿量中一切带 \dagger 与不带 \dagger 数目分歧的项， \hbar \omega_q=\sqrt{8 E_C E_J}-E_C .熟悉非线性光学的读者可以看出这一哈密顿量中的第二项代表Kerr非线性，不外在超导比特中这类非线性（非简谐性）称为Lamb shift。至此我们获得了一个最典范的Transmon的等效哈密顿量。

可调谐超导量子比特（SQUID)

超导比特虽然好用，可是其频次和能级随着制造竣事就牢固了，这对于一些尝试来说并不方便。为此，另一种可调谐超导量子比特被提出，其结构以下图

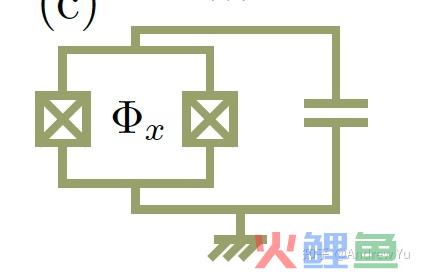
与超导比特一样，都是约瑟夫森结与电容并联，但是约瑟夫森结被替换为了两个自力的约瑟夫森结的并联，并在中心加上由外线圈发生的磁通。这类结构会致使超导相位在两个结之间发生干与，从而等效可以改变比特能级。我们来具体看一下这类机制：首先写出系统哈密顿量 \hat{H}_{\mathrm{T}}=4 E_C \hat{n}^2-E_{J 1} \cos \hat{\varphi}_1-E_{J 2} \cos \hat{\varphi}_2\\第一项代表两个约瑟夫森结与电容并联的总电场能，后两项代表两个约瑟夫森结的磁场能。但是，由于我们制定了约瑟夫森结之间的磁通，量子相位干涉会致使 \hat{\varphi}_1-\hat{\varphi}_2=2 \pi \Phi_x / \Phi_0(\bmod 2 \pi)\\在此根本上，经过和差化积公式便可以获得

\hat{H}_{\mathrm{T}}=4 E_C \hat{n}^2-E_J\left(\Phi_x\right) \cos \left(\hat{\varphi}-\varphi_0\right)\\E_J\left(\Phi_x\right)=E_{J \Sigma} \cos \left(\frac{\pi \Phi_x}{\Phi_0}\right) \sqrt{1+d^2 \tan ^2\left(\frac{\pi \Phi_x}{\Phi_0}\right)}\\其中 \varphi=(\varphi_1+\varphi_2)/2 为两个约瑟夫森结的均匀相位。这类可调谐超导比特(SQUID)虽然好用，可是也有一大弱点，就是由于磁通的涨落会致使其退相关。在比来的尝试中，SQUID用的越来越少了，首要就是出于这一斟酌。

总结

本文先容了约瑟夫森结的道理，以及约瑟夫森结与外电路耦合后发生的超导比特和SQUID。这一部份内容推导较多，不外都不具有理论上的应战性。我感觉最重要的是需要了解Transmon的逻辑：电容耦合致使电荷涨落，从而致使退相关，是以我们希望减小单元电荷致使的能级变化，减小 E_C ,而这会致使 E_J 相对而言增大。这一参数挑选致使磁场能对应的超导相位涨落减小，从而可以对哈密顿量停止小量展开，获得简单的Lamb Shift表达式。