蓝契斯特法则的建模与公式推导

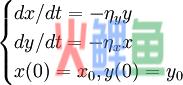
　　遵循蓝氏基本思路，我们可以重新构造基本对抗模型如下：

　　令x(t)表示t时刻红方兵力，y(t)表示t时刻蓝方兵力。假设：(1) 每一方兵力减损率与另一方兵力成正比；(2) 两军士兵都处于双方火力范围内；(3) 不考虑双方支援部队；(4) 双方的初始兵力分别是x0和y0。

　　由以上假设可得，双方作战人数变化的动态模型为：

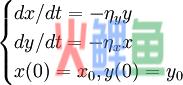　　 　　　　（1）

　　其中：ηx > 0,ηy > 0，均为常数，分别表示红方x和蓝方y的有效攻击系数。

　　对于（1）式，可得：

　　

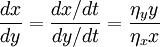
　　移项得：ηxxdx = ηyydy

　　对上式两边分别进行积分，经整理可得：

　　

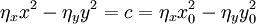
　　这就是著名的蓝氏战略公式。该方程刻画了随着时间推移，双方兵力的动态关系。为了更直观的了解，可以利用相图分析技术，把x(t)和y(t)之间的动态变化关系轨迹，通过笛卡儿直角坐标（x-y）平面（勒内·笛卡尔，Rene Descartes）,形象地刻画出来。显然，运动轨迹是一簇双曲线（具体位置依赖于双方初始兵力情况），如图1所示。双曲线上箭头表示战斗力（人数）随着时间而变化的方向。

　　

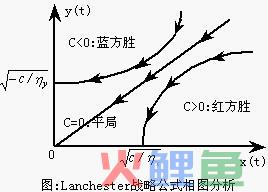
　　从图中可以看出，根据初始条件之不同，可能会出现三种不同的结果（渐进稳定点）。

　　如果双方初始兵力配置满足条件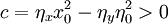：，曲线最终将与x轴相交，也就是说必存在某时刻t1，使蓝方被全歼，y(t1) = 0，此时红方剩余兵力为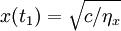，表明红方获胜。

　　同理可知，如果c < 0，则蓝方获胜，剩余兵力为。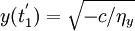

　　如果c=0，双方势均力敌，如果一直火拼下去，双方均无生还之可能（穿过坐标原点）。

　　进一步分析可知，红方要想获胜，必须使初始条件c>0成立，即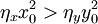。有两种基本途径：1）增加（相对）攻击有效系数ηx；2）增加最初投入兵力x0。

　　公式显示，这两种基本方式对攻击力及最终结果的影响力是不同的。ηx增加一倍，攻击力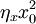（）也增加一倍；但x0增加一倍，则会使攻击力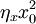（）以平方倍增加，即“兵力对攻击力的影响满足平方律”。这里初始兵力对最终胜败的重要性突显出来了。这正是“蓝氏平方法则”的真正含义，说明兵力增加战斗力将大大增加。

　　二战期间，以美国数学家库普曼（Koopman，1943）为首的美国海军研究组，在“蓝氏平方法则”基础上，扩展成更加完整的战略模型，并利用微分博弈方法和动态最优化方法，计算出各种相对稳定状态下的均衡条件。并从“有效攻击距离”角度，得出了著名的“3倍制胜法则”（准确值为 ，适用于“一对一”对决情形）。据此推导出了保证对局双方力量平衡所需要的初始条件。基本观点是：在双方对决中，一方要想绝对取胜，进攻方必须保证自己的兵力达到对方的3倍以上（“一对一”对决情形），这也说明防御策略在保存力量方面的优势。换言之，要保证取得压倒性胜利，进攻方所投入的兵力必须达到双方总投入兵力比重的73.9%以上；相对应的，如果所投兵力少于总兵力的26.1% (1-73.9%),则必败无疑。此外，只要一方所投入的兵力不少于双方总投入兵力比重的41.7%，就足以维持双方力量的相对平衡，即形成对峙局面。这与人们通常的50%:50% 的直觉观念有一定出入。