抽样分布的类型

　　一、单一样本统计量的抽样分布

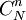
　　当我们要对某一总体的参数进行估计时，就要研究来自该总体的所有可能的样本统计量的分布问题，比如样本均值的分布、样本比例的分布，从而概括有关统计量抽样分布的一般规律。

　　(一)样本均值的抽样分布 　　1．样本均值抽样分布的形成

　　样本均值的抽样分布即所有样本均值的可能取值形成的概率分布。例如，某高校大一年级参加英语四级考试的人数为6000人，为了研究这6000人的平均考分，欲从中随机抽取500人组成样本进行观察。若逐一抽取全部可能样本，并计算出每个样本的平均考分，将会得出很多不完全相同的样本均值，全部可能的样本均值有一个相应的概率分布，即为样本均值的抽样分布。

　　我们知道，从总体的N个单位中抽取一个容量为n的随机样本，在重复抽样条件下，共有N个可能的样本；在不重复抽样条件下，共有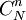 = 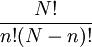个可能的样本。因此，样本均值是一个随机变量。

　　2．样本均值抽样分布的特征

　　从抽样分布的角度看，我们所关心的分布的特征主要是数学期望和方差。这两个特征一方面与总体分布的均值和方差有关，另一方面也与抽样的方法是重复抽样还是不重复抽样有关。

　　无论是重复抽样还是不重复抽样，样本均值的期望值总是等于总体均值μ，即：

　　公式一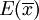： = μ

　　样本均值的方差则与抽样方法有关。在重复抽样条件下，样本均值的方差为总体方差的1/n，即：

　　公式二： =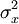

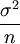
　　在不重复抽样条件下，样本均值的方差为：

　　公式三： =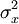

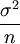
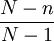
　　从公式二和公式三可以看出两者仅相差系数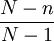，该系数通常被称为有限总体修正系数。在实际应用中，这一系数常常被忽略不计，主要是因为：对于无限总体进行不重复抽样时，由于N未知，此时样本均值的标准差仍可按公式二计算，即可按重复抽样处理；对于有限总体，当N很大而抽样比例n/N很小时，其修正系数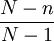=1 - 1，通常在样本容量n小于总体容量N的5％时，有限总体修正系数就可以忽略不计。因此，公式二是计算样本均值方差的常用公式。

　　3．样本均值抽样分布的形式

　　样本均值抽样分布的形式与原有总体的分布和样本容量n的大小有关。

　　如果原有总体是正态分布，那么，无论样本容量的大小，样本均值的抽样分布都服从正态分布。

　　如果原有总体的分布是非正态分布，就要看样本容量的大小。随着样本容量n的增大(通常要求n≥30)，不论原来的总体是否服从正态分布，样本均值的抽样分布都将趋于正态分布，即统计上著名的中心极限定理。

　　(2)虽然总体成绩的分布形态未知，但σ已知，且n=150为大样本，依据中心极限定理可知：样本均值的抽样分布近似服从正态分布。

　　(二)样本比例的抽样分布

　　样本比例即指样本中具有某种特征的单位所占的比例。样本比例的抽样分布就是所有样本比例的可能取值形成的概率分布。例如，某高校大一年级学生参加英语四级考试的人数有6000人，为了估计这6000人中男生所占的比例，从中抽取500人组成样本进行观察，若逐一抽取全部可能样本，并计算出每个样本的男生比例，则全部可能的样本比例的概率分布，即为样本比例的抽样分布。可见，样本比例也是一个随机变量。

　　1．样本比例抽样分布的特征

　　在大样本情况下，样本比例的抽样分布特征可概括如下：

　　无论是重复抽样还是不重复抽样，样本比例p的数学期望总是等于总体比例P，即：

　　公式一：E(p)=P

　　而样本比例p的方差，在重复抽样条件下为：

　　公式二： =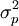

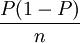
　　在不重复抽样条件下为：

　　 =

　　2．样本比例抽样分布的形式

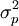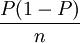
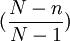
　　样本比例的分布属于二项分布问题，当样本容量n足够大时，即当nP与n(1一P)都不小于5时，样本比例的抽样分布近似为正态分布。

　　二、两个样本统计量的抽样分布

　　如果要对两个总体有关参数的差异进行估计，就要研究来自这两个总体的所有可能样本相应统计量差异的抽样分布。

　　(一)两个样本均值差异的抽样分布

　　若从总体X1和总体X2中分别独立地抽取容量为n1和n2的样本，则由两个样本均值之差 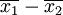的所有可能取值形成的概率分布称为两个样本均值差异的抽样分布。

　　设总体X1和总体X2的均值分别为μ1和μ2，标准差分别为σ1和σ2，则两个样本均值之差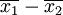的抽样分布可概括为以下两种情况：

　　(1)若总体X1—N(μ1,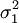)，总体X2—N(μ2,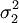)，则

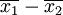　　— N(μ1 − μ2,)

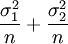　　(2)若两个总体都是非正态总体，当两个样本容量n1和n2都足够大时，依据中心极限定理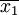，和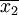分别近似服从正态分布，则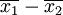— N(μ1 − μ2,)。

　　(二)两个样本比例差异的抽样分布

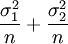　　若从总体X1和总体X2中分别独立地抽取容量为n1和n2的样本，则由两个样本比例之差p1 − p2的所有可能取值形成的概率分布，称为两个样本比例差异的抽样分布。

　　设两个总体的比例分别为P1和P2，当两个样本容量n1和n2都足够大时，根据中心极限定理，p1和p2分别近似服从正态分布，则有

　　p1 − p2—N（P1-P2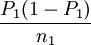，+ ）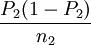